<오라클 성능 고도화 원리와 해법1> Ch05-08 PL/SQL 함수 호출 부하 해소 방안
오라클 성능 고도화 원리와 해법1 - Ch05-08 PL/SQL 함수 호출 부하 해소 방안
다시 한 번 강조하지만, 사용자 정의 함수는 <① 소량의 데이터 조회 시에만 사용>하는 것이 좋다. <② 대용량 데이터를 조회할 때는 부분범위 처리 가능한 상황에서 제한적으로 사용>해야 하며, 되도록이면 <③ 조인 또는 스칼라 서브쿼리 형태로 변환하려는 노력이 필요>하다. 그런데, 구현상 복잡성으로 인해 함수를 도저히 풀 수 없는 경우가 자주있다. <④ 어쩔 수 없을 때는 함수를 쓰되 호출 횟수를 최소화할 수 있는 방법을 강구>해야 한다.
지금부터 설명할 함수 호출 부하 해소 방안을 요약하면 다음과 같다.
- 페이지 처리 또는 부분 범위 처리 활용
- Decode 함수 또는 Case문으로 변환
- 뷰 머지(View Merge) 방지를 통한 함수 호출 최소화
- 스칼라 서브쿼리 캐싱 효과를 이용한 함수 호출 최소화
- Deterministic 함수의 캐싱 효과 활용
- 복잡한 함수 로직을 풀어 SQL로 구현
(1) 페이지 처리 또는 부분범위처리 활용
튜닝 컨설팅을 다니면서 함수 부하 때문에 개발팀에 가장 많이 가이드하는 튜닝 사례는 아래와 같은 경우다.
사실 위 케이스는 함수를 꼭 사용해야만 하는 경우는 아니다. 그런데도 개발 초기에 정해진 표준 규칙에 따라, 코드명을 가져올 때는 함수를 써야만 하는 상황이었다고 가정하자. (가정이라지만 실제 이런 상황에 자주 직면하게된다.)
위처럼 쿼리를 작성하면 최종 결과 건수가 얼마건 간에 조건절에 부합하는 전체 레코드 건수만큼 함수 호출을 일으키고50), 그 결과 집합을 Sort Area 또는 Temp 테이블 스페이스에 저장한다. 그리고 최종 결과 집합 10건만을 사용자에게 전송하게 된다.
아래 처럼 쿼리를 바꾸면, order by 와 rownum에 의한 필터 처리 후 사용자에게 전송하는 최종 결과 집합에 대해서만 함수 호출이 일어난다. 요즘 같은 n-Tier 환경에서는 페이지 처리가 필수다 보니 가장 흔히 접하게 되는 튜닝 사례이므로 반드시 숙지해서 실무에 적용하기 바란다.
페이지 처리를 하지 않더라도 부분 범위 처리가 가능한 상황이라면 클라이언트에게 데이터를 전송하는 맨 마지막 단계에 함수 호출이 일어나도록 함(-> 위와 같이 맨 바깥쪽 select-list에 함수를 기술하면 됨)으로써 큰 성능 개선을 이룰 수 있다.
(2) Decode 함수 또는 Case문으로 변환
함수가 안쪽 인라인 뷰에서 order by절에 사용된다든가, 전체 결과 집합을 모두 출력하거나, insert…select 문에서 사용된다면 다량의 함수 호출을 피할 수 없다. 그럴 때는 함수 로직을 풀어서 decode, case문으로 전환하거나 조인문으로 구현할 수 있는지 먼저 확인해야 한다. 함수 로직이 복잡하거나 프로젝트 규칙상 함수를 사용해야만 한다면 함수에 입력되는 값의 종류가 얼마나 되는지 확인해보기 바란다. 만약 값의 종류가 많지 않다면 함수를 그대로 둔 채 스칼라 서브쿼리의 캐싱 효과를 이용하는 것만으로도 큰 효과를 볼 수 있기 때문이다.
물론 함수를 사용하는데 따른 장점도 있다. 함수를 사용하면 분류체계가 바뀌더라도 SQL들을 찾아 일일이 바꾸지 않아도 된다. 함수 내용만 바꿔주면 되기 때문이다. 하지만 굳이 함수를 이용하지 않더라도 정보 분류 및 업무 규칙, 규정들을 테이블화해서 관리한다면 매번 쿼리를 바꾸지 않고도 함수가 갖는 장점들을 그대로 가져올 수 있다. 지금 보고 있는 사례에서 상품 분류가 바뀔 수 있다면 아래처럼 시장 코드와 증권 그룹 코드별 분류명을 메타 정보로써 관리하는 테이블을 만들어 사용하면 된다.
분류 순서 테이블과의 조인 때문에 성능이 느려질 것이라고 생각했을지 모르지만 전혀 그렇지 않았다. 0.68초만에 수행된 것을 볼 수 있다. 100만 건 그대로 조인을 실시하면 당연히 느려지겠지만(이 역시도 해시 조인으로 처리하면 빠르게 수행된다.) group by를 먼저 수행해 20건으로 압축된 결과 집합을 가지고 조인하므로 성능을 전혀 떨어뜨리지 않는다.
(3) 뷰머지(View Merge) 방지를 통한 함수 호출 최소화
어떤 이유에서건 함수를 풀어 조인문으로 변경하기 곤란한 경우가 분명히 있다. 그럴 때는 함수를 그대로 둔 채 함수 호출 횟수를 줄이려는 노력을 해야 하는데, 어떤 방법들이 있는지 살펴보자.
하지만 수행해보면 속도가 전혀 줄지 않았다. 옵티마이저, 그 중에서도 Query Transformer에 의해 뷰 머지(View Merge)가 발생했기 때문이다. 즉 뷰 머지 때문에 인라인 뷰로 묶기 이전 상태로 되돌아간 것이다. 아래처럼 뷰머지가 발생하지 못하도록 no merge 힌트를 사용하면 기대했던 효과가 나타난다.
no merge 힌트를 사용하지 않더라도 뷰 내에 rownum을 사용하면 옵티마이저는 절대 뷰 머지를 시도하지 않는다. rownum을 포함하는 뷰를 메인 쿼리와 merge하면 결과가 틀릴 수 있기 때문에 주의해야 한다.
더 빠르게 수행되도록 튜닝할 방법은 없는 걸까? 스칼라 서브쿼리의 캐싱 효과를 이용하는 방법이 있다.
(4) 스칼라 서브쿼리의 캐싱 효과를 이용한 함수 호출 최소화
2권 조인 원리을 설명하는 장에서 다룰 내용이지만 간단히 설명하자면 스칼라 서브쿼리를 사용하면 오라클은 그 수행 횟수를 최소화하려고 입력값과 출력값을 내부 캐시(Query Execution Cache)에 저장해둔다. 스칼라 서브쿼리에 있어 입력값은, 거기서 참조하는 메인 쿼리의 컬럼값을 말한다.
서브쿼리가 수행될 때마다 입력값을 캐시에서 찾아보고 거기 있으면 저장된 출력값을 리턴하고, 없으면 쿼리를 수행한 후 입력값과 출력값을 캐시에 저장해두는 원리다. 이 기능을 함수 호출 횟수를 줄이는 데 사용할 수 있는데, 함수를 Dual 테이블을 이용해 스칼라 서브쿼리로 한번 감싸는 것이다. 특히, 함수 입력값의 종류가 적을 때 이 기법을 활용하면 함수 호출 횟수를 획기적으로 줄일 수 있다.
함수 호출 횟수를 20번으로 예상했는데, 왜 이처럼 터무니 없게 많이 수행된 것일까? 해시 충돌이 발생했기 때문이다. 해시 충돌이 발생하면 기존 엔트리를 밀어내고 새로 수행한 입력값과 출력값으로 대체할 것 같지만, 오라클은 기존 캐시 엔트리를 그대로 둔 채 스칼라 서브쿼리만 한번 더 수행하고만다. 따라서 해시 충돌이 발생한 입력값이 반복적으로 입력되면 스칼라 서브쿼리를 사용하기 전처럼 여전히 쿼리가 반복 수행되기 때문에 위와 같은 현상이 발생하는 것이다.
필자가 공동 번역한 ‘비용 기반의 오라클 원리(원제: Cost-Based Oracle Fundamentals)’ 저자인 조나단 루이스 설명에 의하면 8i, 9i에서는 256개 엔트리를 캐싱하고, 10g에서는 입력과 출력값 크기, _query_execution_cache_max_size 파라미터에 의해 캐시 사이즈가 결정된다고 한다. 이 Hidden 파라미터 값을 증가시킨 후 테스트해보자.
이처럼 insert ••• select문이거나 부분범위 처리 활용 없이 전체 데이터를 출력해야 하는 상황에서 함수 호출 때문에 성능이 크게 떨어진다면 스칼라 서브쿼리를 활용함으로써 성능을 획기적으로 개선할 수 있다.**
아래는 ‘(1) 페이지 처리 또는 부분범위 처리 활용’에서 보았던 쿼리의 함수 호출 부분을 스칼라 서브쿼리로 덧씌운 것이다. 앞에서는 함수 호출 부분을 맨 바깥쪽 select-list에 기술함으로써 성능을 개선할 수 있음을 설명했지만, 페이지 처리 또는 부분범위 처리가 불가능한 상황에서는 효과가 전혀 없다. 그럴 때 아래처럼 스칼라 서브쿼리를 활용함으로써 큰 효과를 얻을 수 있다.
이 기법은 입력값의 종류가 소수여서 해시 충돌 가능성이 적은 함수에만 적용해야 하며, 그러지 않을 경우에도 오히려 CPU 사용률만 높이게 되므로 먼저 원리를 충분히 이해하고 나서 효과가 확실한 경우에만 사용하기 바란다.
(5) Deterministic 함수의 캐싱 효과 활용
10gR2에서 함수를 선언할 때 Deterministic 키워드를 넣어 주면 스칼라 서브쿼리를 덧입히지 않아도 캐싱 효과가 나타난다. 함수의 입력값과 출력값은 CGA(Call Global Area)에 캐싱된다. CCA에 할당된 값은 데이터베이스 Call 내에서만 유효하므로 Fetch Call이 완료되면 그 값들은 모두 해제된다. 따라서 Deterministic 함수의 캐싱 효과는 데이터베이스 Call 내에서만 유효하다. 반면, 스칼라 서브쿼리에서의 입력, 출력값은 UGA에 저장되므로 Fetch Call에 상관없이 그 효과가, 캐싱되는 순간부터 끝까지 유지된다.
과도한 함수 호출 때문에 성능 이슈를 경험하고 있다면, 위 사실을 접하는 순간 전광석화처럼 떠오르는 생각이 있다. 함수 호출 횟수를 줄일 목적으로 함수를 Deterministic으로 선언하면 되겠다고 생각할 것이다. 하지만 앞에서 PL/SQL 함수의 특징을 설명했듯이, 함수 안에 쿼리문을 포함하고 있다면 그 함수는 일관성이 보장되지 않는다. 즉, 같은 입력값에 대해 언제라도 다른 출력값을 낼 수 있다는 뜻이다.
이것은 Deterministic 함수일 때도 마찬가지다. Deterministic 키워드는 그 함수가 일관성 있는 결과를 리턴함을 선언하는 것일 뿐, 그것을 넣었다고 해서 일관성이 보장되는 것은 아니다. 단지, 함수를 구현한 개발자가 그 함수의 일관성 있는 결과 출력을 책임진다는 선언적 의미만을 갖는다. 오라클이 Deterministic 함수일 때만 캐싱 기능이 작동하도록 구현한 것도 그 때문이다.52)
결론적으로 말해, 앞에서 본 ACCUM 함수는 시점과 무관하게 항상 일관성 있는 결과를 출력하므로 캐싱 효과를 위한 Deterministic 함수의 올바른 활용 사례지만, 함수가 쿼리 문을 포함할 때는 캐싱 효과를 위해 함부로 Deterministic으로 선언해선 안된다. 만약 select 문을 포함한 함수를 Deterministic으로 선언하면 일관성 측면에서 의도하지 않은 결과를 초래할 수 있으므로 주의해야 한다. 데이터베이스 Call 성능 문제를 다루면서 이 부분을 더 깊이 설명하는 것은 적절치 않은 것 같아 부록에서 자세히 설명하였으므로 참고하기 바란다.
(6) 복잡한 함수 로직을 풀어 SQL로 구현
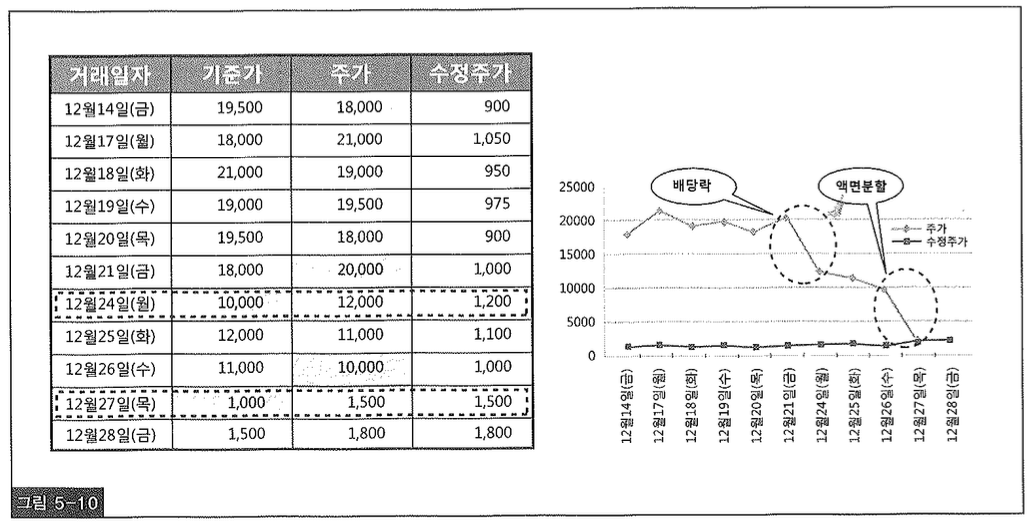
복잡한 함수 로직을 풀어 SQL만으로 해결한 사례를 소개하면서 본 장을 마치려고 한다. 증권 회사에서 튜닝한 사례인데, 먼저 ‘수정주가’에 대한 개념을 살펴보자. 어떤 주식에 대해 유•무상 증자에 의한 권리락, 배당에 의한 배당락, 액면변경 등이 발생하면 전일 주가와 당일 주가 사이에 단층이 생겨 주가의 연속성을 잃게된다. 따라서 현재와 과거 주가를 비교할 때는 수정주가를 자주 사용한다. 즉, 조회 시점 기준으로 과거 주가를 수정하는 것이다. 그런 이벤트가 발생했을 때 전일 종가를 그대로 당일 기준가로 사용하면 거래가 시작되자마자 바로 상한가 또는 하한가를 기록해 주가 등락 정보를 왜곡하게 되므로 당일 기준가를 조정하는 시장 조치를 실시한다. 그 때의 당일 주가와 전일 주가의 수정 비율을 구하고, 이 비율을 주가에 반영함으로써 수정주가를 구한다.
수정주가는, 거래일 이후에 발생했던 주가 수정 비율을 모두 곱해서 구한다. 예를들어, 그림5-10 좌측에 있는 표에서 12월 14일 수정주가는 24일의 수정비율 0.5(=10,000/20,000)와 27일의 수정비율 0.1(=1,000/10,000)을 곱한 0.05를 적용해서 구한다(18,000 x 0.05 = 900).
업무가 복잡하다 보니 이 회사에서는 수정주가를 구하는 함수를 사용하고 있었다. 당연히 넓은 검색 기간과 많은 종목을 대상으로 조회하면 성능이 급격히 저하된다. 그래서 성능 문제를 해결하려고 매일 야간 배치로 수정주가를 미리 구해 저장해두고 있었다. 과거 10년치를 보관하는 많은 집계 테이블 중 주가를 속성으로 갖는 테이블들을 매일 업데이트하는 것이다.
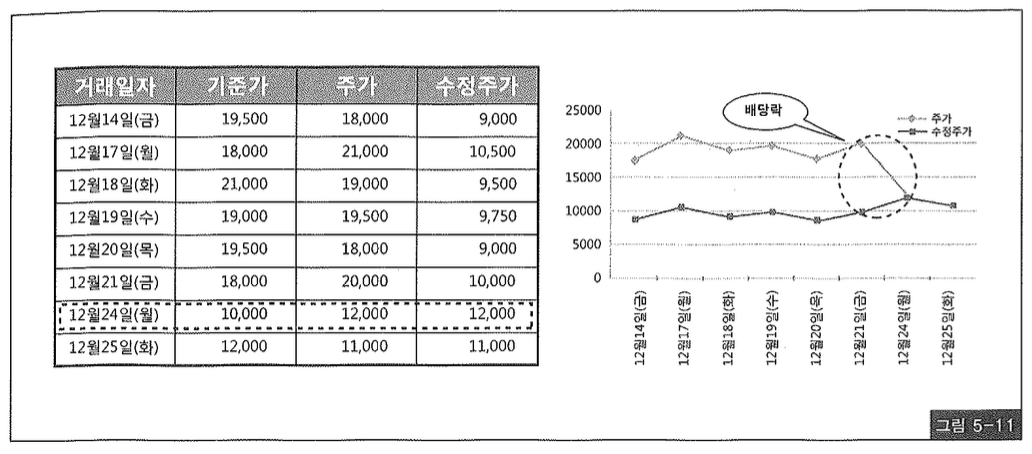
또 다른 문제는, 그렇게 미리 구해둔 수정주가는 가장 마지막 이벤트가 발생한 이후 시점으로 조회할 때만 유효하다는 사실이다. 조회 범위 종료일자가 가장 마지막 이벤트 발생보다 앞선 시점이면 여전히 함수를 사용할 수 밖에 없다. 예를들어, 그림5-11은 12월 25일(화)시점으로 조회하는 경우인데, 앞 표에서 12월 27일에 발생한 수정비율은 수정 주가에 반영되지 않아야 하므로 미리 구해둔 수정주가는 의미 없게 된다.
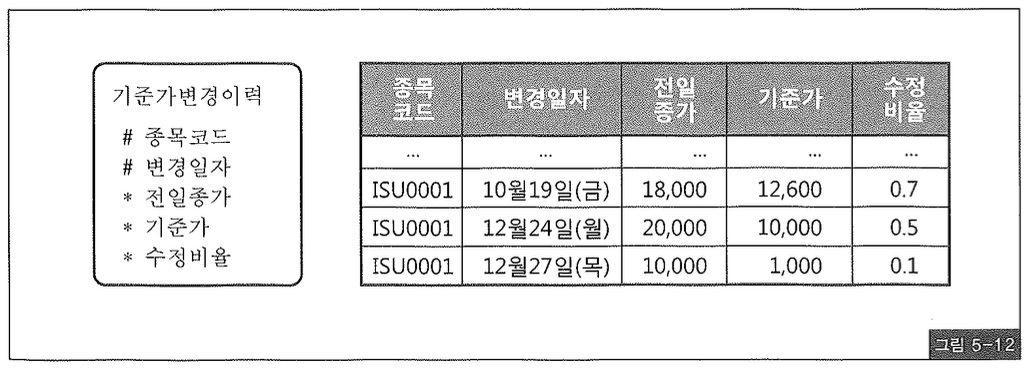
주가에 영향을 미치는 이벤트가 발생할 때마다 기준가 변경 이력을 관리하는 테이블과 사례 데이터는 그림5-12와 같다.
그리고 위 테이블을 이용해 수정주가를 구하는 함수는 다음과 같다.
함수 내용을 분석해보면 알 수 있듯이 거래일자 다음날부터 조회일자 이전까지의 수정비율을 모두 곱하는 로직이다. 즉, 누적곱을 구하고자 하는 것이다. 누적합은 분석 함수를 이용해 쉽게 구할 수 있으나 누적곱을 구하는 방법을 찾지 못해 위와 같은 함수를 구현했던 것이다. 함수를 사용하지 않고 수정주가를 구하는 방법을 찾아야만 한다. 그러지 않고는 성능을 개선하기 어렵다.
아래는 특정 종목에 대한 2008년 1년치 거래 데이터를 조회하면서 위 함수를 이용해 수정주가를 확인하는 쿼리다.
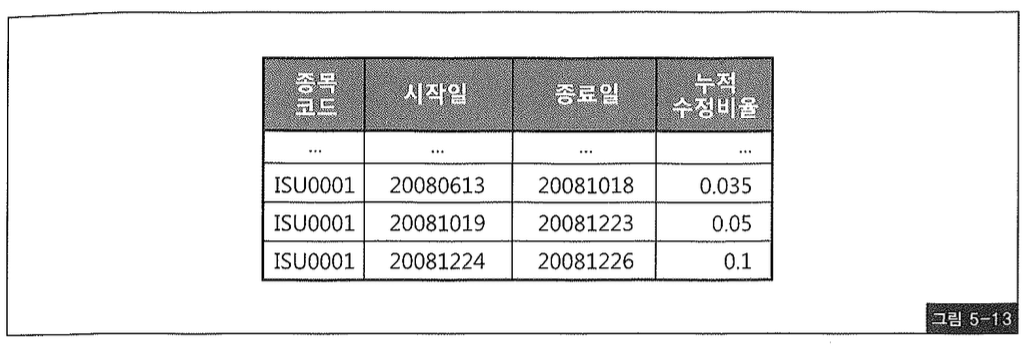
쿼리에 사용된 일별 종목 주가는 [종목코드+거래일자]를 PK로 갖는 테이블로서, 일자별로 모든 종목에 대한 당일 종가가 구해져 있다. 그림5-13에서 표현한 선분 이력 처럼 각 일자 구간(시작일 ~ 종료일) 별로 누적 수정비율을 갖는 중간집합을 생성할 수만 있다면 일별 종목 주가 테이블과의 조인을 통해 의외로 쉽게 문제를 풀 수 있다.
아래 쿼리가 최종 튜닝된 결과인데, 중간에 EXP(지수, Exponential)와 LN(자연 로그, Natural Log) 함수를 포함하는 인라인 뷰가 그림5-13과 같은 형태의 중간집합을 가공해내는 부분이다. 즉, 누적곱을 구하는 쿼리다. 나머지는 이 중간집합과 일별 종목 주가 테이블을 조인하는 것에 불과하다.
이 방식을 적용함으로써 실시간 쿼리의 함수 호출 부하를 해소했음은 물론, 수정주가를 미리 구해 저장해두려고 매일 과거 10년치 데이터를 갱신하는 배치 프로그램을 더는 수행할 필요가 없게 되었다.
사실 위 튜닝 사례를 정확히 이해하려면 주식에 대한 사전 지식이 필요하다. 주식투자를 하지 않는 독자라면 다소 어려울 수 있는 내용이지만 굳이 이해하려고 노력할 필요는 없다. 다만, 함수 호출에 의한 부하가 얼마나 심각한 것인지, 그리고 이를 풀어냄으로써 얼마만큼 획기적인 성능개선을 이룰 수 있는지, 그 원리를 이해했다면 성공이다. 이 원리를 각자 처한 개발 업무에 적용함으로써 많은 성능 문제들을 해결할 수 있기를 바란다.