<오라클 성능 고도화 원리와 해법2> Ch01-04 테이블 Random 액세스 부하

오라클 성능 고도화 원리와 해법2 - Ch01-04 테이블 Random 액세스 부하

SQL 튜닝, 그 중에서도 인덱스 원리를 공부하면서 누구나 두 번 놀라게 된다. 첫째로는 인덱스를 효과적으로 활용했을 때 쿼리 성능이 얼마나 빨라지는지를 느꼈을 때이고, 둘째로는 대량의 데이터를 인덱스를 통해 액세스할 때 쿼리 성능이 얼마나 느려지는지를 느꼈을 때다.

본 절에서는 대량의 데이터를 처리할 때 테이블 랜덤 액세스가 가장 큰 부하 요인으로 작용하는 원인을 자세히 설명하고, 5절과 6절에서 이를 해소하기 위한 튜닝 방안을 소개한다.

(1) 인덱스 ROWID에 의한 테이블 액세스

앞 절에서 다양한 인덱스 스캔 방식에 대해 살펴봤는데, 쿼리에서 참조되는 컬럼이 인덱스에 모두 포함되는 경우가 아니라면 인덱스 스캔 이후 테이블 랜덤 액세스가 일어난다. 아래 실행 계획에서 ‘Table Access By Index ROWID’라고 표시된 부분을 말하며, 지금부터 그 내부 메커니즘을 자세히 살펴보자.

물리적 주소? 논리적 주소?

인덱스에 저장된 ROWID는 흔히 ‘물리적 주소 정보’라고 일컬어지는데, 오브젝트 번호, 데이터 파일 번호, 블록 번호 같은 물리적 요소들로 구성되어 있기 때문일 것이다. 하지만 보는 시각에 따라서는 ‘논리적 주소 정보’라고 표현하기도 한다. ROWID가 물리적 위치 정보로 구성되지만 인덱스에서 테이블 레코드로 직접 연결되는 구조는 아니기 때문이다.

메인 메모리 DB와의 비교

메인 메모리 DB(MMDB)에 대해 들어본 적이 있을까? 말 그대로 데이터를 모두 메모리에 로드해놓고 메모리를 통해서만 I/O를 수행하는 DB라고 할 수 있다. 그런데 잘 튜닝된 OLTP 성 오라클 데이터베이스라면 버퍼 캐시 히트율이 99% 이상이므로 대부분 디스크를 경유하지 않고 메모리 상에서 I/O를 수행할 텐데도 메인 메모리 DB만큼 빠르지는 않다. 특히 대량의 테이블을 인덱스를 통해 액세스할 때는 엄청난 차이가 난다. 왜 그럴까?

메인 메모리 DB도 벤더에 따라 내부적으로 다른 아키텍처를 사용하겠지만 필자가 아는 어떤 제품의 아키텍처를 소개함으로써 방금 던진 질문에 대한 답을 찾고자 한다.

메인 메모리 DB에서 인스턴스를 기동하면 디스크에 저장된 데이터를 버퍼 캐시로 로딩하고 이어서 인덱스를 실시간으로 만든다. 이때 인덱스는 오라클처럼 디스크 상의 주소 정보를 담는 게 아니라 메모리 상의 주소 정보, 즉 포인터를 담는다. 프로그래머라면 누구나 포인터 개념을 공부하므로 포인터에 의한 액세스가 얼마나 빠른지는 잘 알 것이다.

메모리 상에서 데이터를 찾아가는데 있어 포인터만큼 빠른 방법은 없으며 그 비용은 거의 0에 가깝다. 따라서 인덱스를 경유해 테이블을 액세스하는데 대한 비용이 오라클과 비교할 수 없을 정도로 낮다.

질문에 대한 답이 무엇인지, 이해했으리라 믿는다. 오라클은 테이블 블록이 수시로 버퍼 캐시에 서 밀려났다가 다시 캐싱되며, 그때마다 다른 공간에 캐싱되기 때문에 인덱스에서 직접 포인터로 연결할 수 없는 구조다. 대신 디스크 상의 블록 위치 정보, 즉 DBA(Data Block Address)를 해시키 값으로 삼아 해싱 알고리즘을 통해 버퍼 블록을 찾는다. 매번 위치가 달라지더라도 캐싱되는 해시 버킷만큼은 고정적이다.

여기서 메인 메모리 DB의 우월성을 강조하고자 하는 것은 아니며(메인 메모리 DB는 데이터 볼륨이 그리 크지 않으면서, 기존 디스크 DB로는 도저히 만족할 수 없을 정도의 빠른 트랜잭션 처리가 요구되는 업무에서만 제한적으로 사용되고 있음), 우리가 사용하는 오라클 데이터베이스에서 인덱스 rowid에 의한 테이블 액세스가 생각만큼 빠르지 않은 이유를 설명하려는 것이다.

rowid는 우편 주소에 해당

비유하자면, 오라클에서의 rowid는 우편 주소에 해당하고, 메인 메모리 DB에서 사용하는 포인터는 전화번호에 해당한다. 전화는 물리적으로 연결된 구조여서 전화번호만 누르면 곧바로 상대방과 직접 통화할 수 있지만, 우편 주소는 봉투에 적힌 대로 우체부 아저씨가 일일이 찾아다니는 구조이므로 전화와는 비교할 수 없이 느리다.

인덱스 rowid에 의한 테이블 액세스 구조

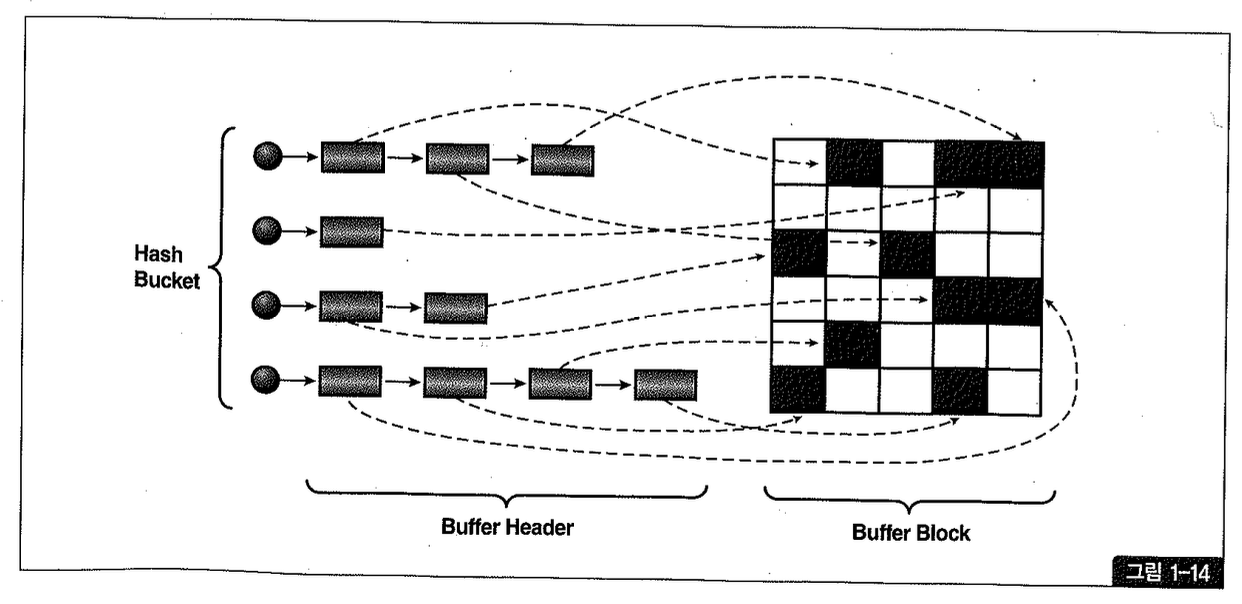
1권 1장 3절에서 설명한 것처럼(잠시 후 다시 자세히 설명함) 오라클도 포인터로 빠르게 액세스하는 버퍼 Pinning 기법을 사용하지만 반복적으로 읽힐 가능성이 큰 블록에 대해서만 일부 적용하고 있다. 이 메커니즘의 도움을 받지 않은 일반적인 인덱스 rowid에 의한 테이블 액세스가 실제로 얼마나 고비용인지, 1권 1장에서 보았던 그림 1-148)을 보면서 상기해보자.

오라클에서 하나의 레코드를 찾아가는데 있어 가장 빠르다고 알려진 rowid에 의한 테이블 액세스가 경우에 따라서는(-> 위 설명은 가장 최악의 상황을 가정한 것임) 이렇게까지 고비용이라는 사실을 상기시키기 위함이다.

요약하면, 인덱스 rowid는 테이블 레코드와 물리적으로 연결돼 있지 않기 때문에 인덱스를 통한 테이블 액세스는 생각보다 고비용 구조다. 설령 모든 데이터가 메모리에 캐싱돼 있더라도 테이블 레코드를 찾기 위해 매번 DBA를 해싱하고 래치 획득 과정을 반복해야 하기 때문이며, 동시 액세스가 심할 때는 래치와 버퍼 Lock에 대한 경합까지 발생한다.

앞으로 실행 계획에서 아래와 같이 ‘Table Access By Index ROWID’ 오퍼레이션을 볼 때면 위에서 설명한 복잡한 처리 과정을 항상 머리속에 떠올리기 바란다.

(2) 인덱스 클러스터링 팩터

군집성 계수(= 데이터가 모여 있는 정도)

클러스터링 팩터(clustering Factor, 이하 CF)는 ‘군집성 계수’ 쯤으로 번역될 수 있는 용어로서, 특정 컬럼을 기준으로 같은 값이 갖는 데이터가 서로 모여 있는 정도를 의미한다. CP가 좋은 컬럼에 생성한 인덱스는 검색 효율이 매우 좋은데, 예를 들어 「거주지역= ‘제주’」에 해당하는 고객 데이터가 물리적으로 근접해 있다면 흩어져 있을 때보다 데이터를 찾는 속도가 빨라지게 마련이다.

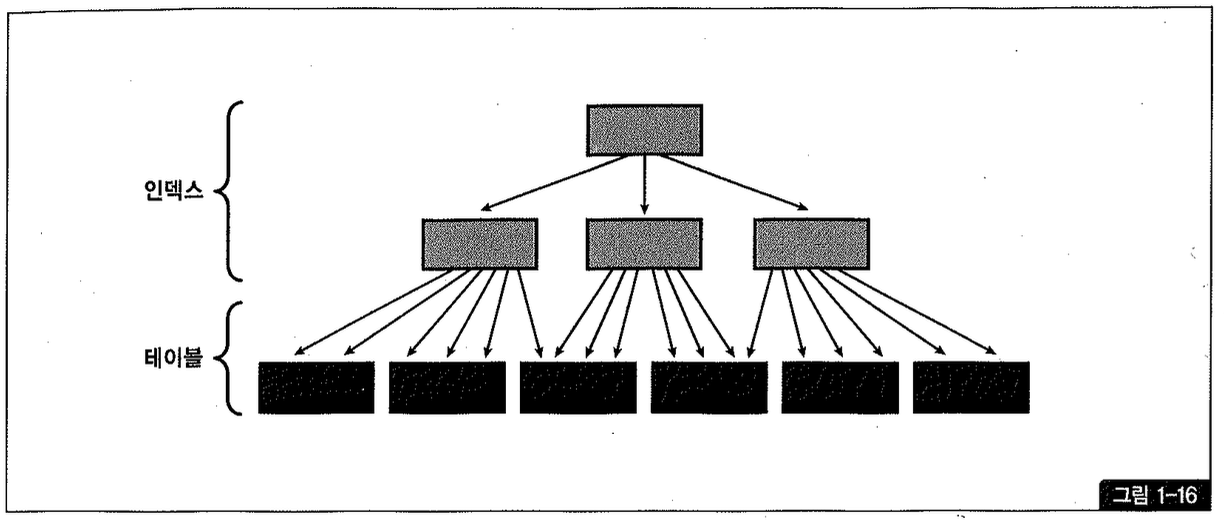
그림1-16은 인덱스 클러스터링 팩터가 가장 좋은 상태를 도식화한 것으로서, 인덱스 레코드 정렬 순서와 거기서 가리키는 테이블 레코드 정렬 순서가 100% 일치하는 것을 볼 수 있다.

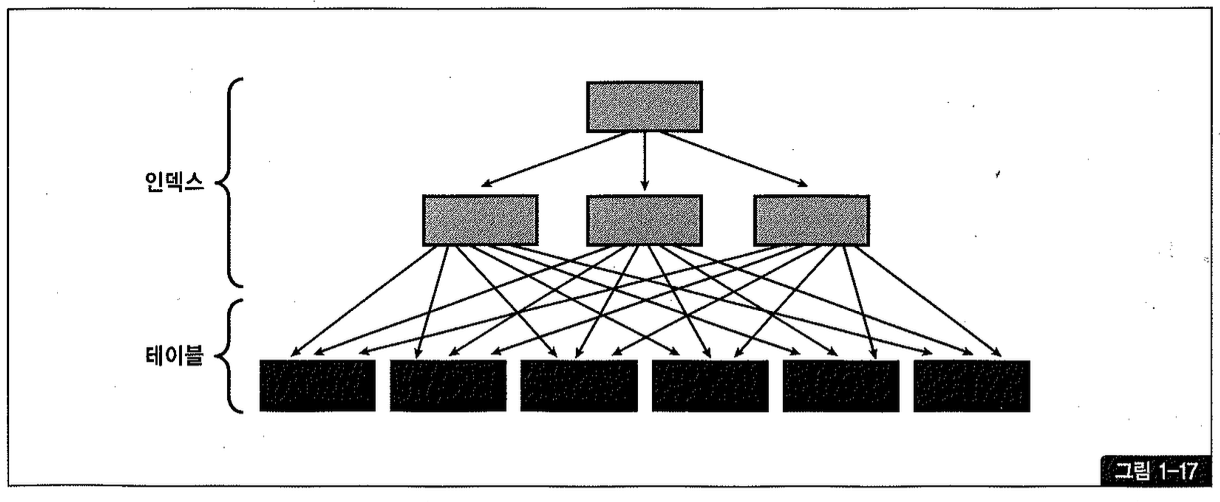
반면 그림1-17은 인덱스 클러스터링 팩터가 가장 안 좋은 상태를 도식화한 것으로서, 인덱스 레코드 정렬 순서와 테이블 레코드 정렬 순서가 전혀 일치하지 않는다.

클러스터링 팩터 조회

CF는 데이터가 모여 있는 정도를 의미한다고 했는데, 오라클은 이를 어떻게 수치화해서 표현할까?

clustering factor 수치가 테이블 블록(table_blocks)에 가까울수록 데이터가 잘 정렬되어 있음을 의미하고, 레코드 개수(numrows)에 가까울수록 흩어져 있음을 의미한다. 인덱스 통계를 수집할 때 clustering factor 계산을 위해 오라클이 사용하는 아래 로직을 보고나면 이유를 쉽게 알 수 있다.

1. counter 변수를 하나 선언한다.
2. 인덱스 리프 블록을 처음부터 끝까지 스캔하면서 인덱스 rowid로부터 블록 번호를 취한다.
3. 현재 읽고 있는 인덱스 레코드의 블록 번호가 바로 직전에 읽은 레코드의 블록 번호와 다를 때마다 counter 변수 값을 1씩 증가시킨다.
4. 스캔을 완료하고서, 최종 counter 변수 값을 clustering factor로서 인덱스 통계에 저장한다.

이런 식으로 측정된 CF 값은 옵티마이저가(테이블 Full Scan과 비교해) 인덱스 Range Scan을 통한 테이블 액세스 비용을 계산하기 위해 사용된다. 참고로, 00 비용 모델일 때) 인덱스를 이용한 테이블 액세스 비용을 계산하기 위해 오라클이 사용하는 공식은 다음과 같다. 자세한 설명은 3장 7절을 참고하기 바란다.

• blevel: 리프 블록에 도달하기 전 읽게 될 브랜치 블록 개수 • 유효 인덱스 선택도: 전체 인덱스 레코드 중에서 조건절을 만족하는 레코드를 찾기 위해 스캔할 것으로 예상되는 비율(%) • 유효 테이블 선택도: 전체 레코드 중에서 인덱스 스캔을 완료하고서 최종적으로 테이블을 방문할 것으로 예상되는 비율(%)

클러스터링 팩터와 물리적 I/O

“인덱스 CF가 좋다”고 하면 인덱스 정렬 순서와 테이블 정렬 순서가 서로 비슷하다는 것을 말한다. 인덱스 레코드는 항상 100% 정렬된 상태를 유지하는데, 테이블 레코드도 이와 비슷한 정렬 순서를 갖는다면 값이 같은 레코드들이 서로 군집해있음을 뜻한다. 이는 궁극적으로 물리적인 디스크 I/O 횟수를 감소시키는 효과를 가져다 준다.

오라클에서 I/O는 블록 단위로 이루어 지므로 인덱스를 통해 하나의 레코드를 읽으면 같은 블록에 속한다면 다른 레코드들도 함께 캐싱되는 결과를 가져올 것이고, CF가 좋은 인덱스였다면(= 같은 값들이 서로 군집해 있다면) 그 레코드들도 가까운 시점에 읽힐 가능성이 높다(그림1-16), 따라서 인덱스를 스캔하면서 읽는 테이블 블록들의 캐시 히트율이 높아지므로 물리적인 디스크 I/O 횟수가 감소하게 되는 것은 당연한 이치다.

반대로, 값이 같은 레코드들(예: 거주지역=’제주’)이 서로 멀리 떨어져 있다면 논리적으로 더 많은 블록을 읽어야 하므로(~ 이유는 바로 뒤에서 설명함) 물리적인 디스크 I/O 횟수도 같이 증가하게 된다 (그림1-17). 설상가상으로, 앞서 읽었던 테이블 블록을 다시 방문하고자 할 때 이미 캐시에서 밀려나 고 없 다 면 같 은 블 록 을 디 스 크 에 서 여 러 번 읽 게 되 므 로 I / O 효 율 은 더 나 빠 질 것 이 다.

클러스터링 팩터와 논리적 I/O

인덱스 CF는 단적으로 말해, 인덱스를 경유해 테이블 전체 로우를 액세스할 때 읽을 것으로 예 상되는 논리적인 블록 개수를 의미한다. 따라서 CF가 가장 좋을 때는 인덱스 통계에 나타나는 clustering factor가 전체 테이블 블록 개 수 와 일치하고, 가장 안 좋을 때는 총 레코드 개수 와 일치한다. 참고로, 모든 블록에 레코드가 하나씩만 저장돼 있다면 clustering factor는 항상 총 레코드 개수와 일치할 것이다.

물리적 I/O 계산을 위해 논리적 I/O를 측정

오라클은 인덱스가 가리키는 데이터의 흩어짐 정도를 인덱스 비용 계산식에 표현하기 위해 CF를 고안하였다. 그런데 옵티마이저가 사용하는 비용 계산식은 기본적으로 물리적인 I/O만을 고려(논리적 I/O가 모두 물리적 I/O를 수반한다고 가정)하므로 CF도 궁극적으로 물리적 I/O 비용을 평가하기 위한 수단이라고 말할 수 있다. 하지만 논리적 I/O가 100% 물리적 I/O를 수반한다는 가정은 매우 비현실적이다. 특히, 앞서 읽었던 테이블 블록을 다시 읽을 때 실제로는 캐싱된 블록을 읽을 가능성이 훨씬 높다. 한번 읽었던 테이블 블록이 버퍼 캐시에서 밀려나지 않도록 충분한 버퍼 캐시를 확보한 상태에서 인덱스를 통해 전체 테이블 레코드를 읽는 경우를 가정해보자. 그러면 위에서 본 t object name idx 인덱스의 clustering factor 수치(24,936)는 실제 발생할 수 있는 물리적 I/O 횟수와 전혀 다른 값이 될 수 있다. 물리적으로 읽어야 할 전체 테이블 블록 개수는 고정되어 있기 때문이다. 그럼에도 캐싱 효과를 예측하기가 매우 어렵기 때문에 옵티마이저는 CF를 통해 계산된 논리적 I/O 횟수를 그대로 물리적 I/O 횟수로 인정하고 인덱스 비용을 평가하는 것이다. 결론적으로 말해, 인덱스 통계에서 볼 수 있는 clustering factor는 인덱스를 통해 테이블을 액세스할 때 예상되는 논리적 I/O 개수를 더 정확히 표현하고 있다.

버퍼 Pinning에 의한 논리적 I/O 감소 원리

인덱스의 CF에 따라 논리적인 블록 I/O 개수가 심하게 차이나는 이유는 무엇일까? 그 이유는, 인덱스를 통해 액세스되는 하나의 테이블 버퍼 블록을 Pinning하기 때문이다.

버퍼 Pinning에 대해서는 1권(장 3절 4행)에서 자세히 설명했지만 간단히 요약하면, 방금 액세스한 버퍼에 대한 Pin을 즉각 해제하지 않고 데이터베이스 Call 내에서 계속 유지하는 기능이라고 할 수 있다. 따라서 연속된 인덱스 레코드가 같은 블록을 가리킨다면, 래치 획득 과정을 생략하고 버퍼를 Pin한 상태에서 읽기 때문에 논리적인 블록 읽기(Logical Reads) 횟수가 증가하지 않는다.

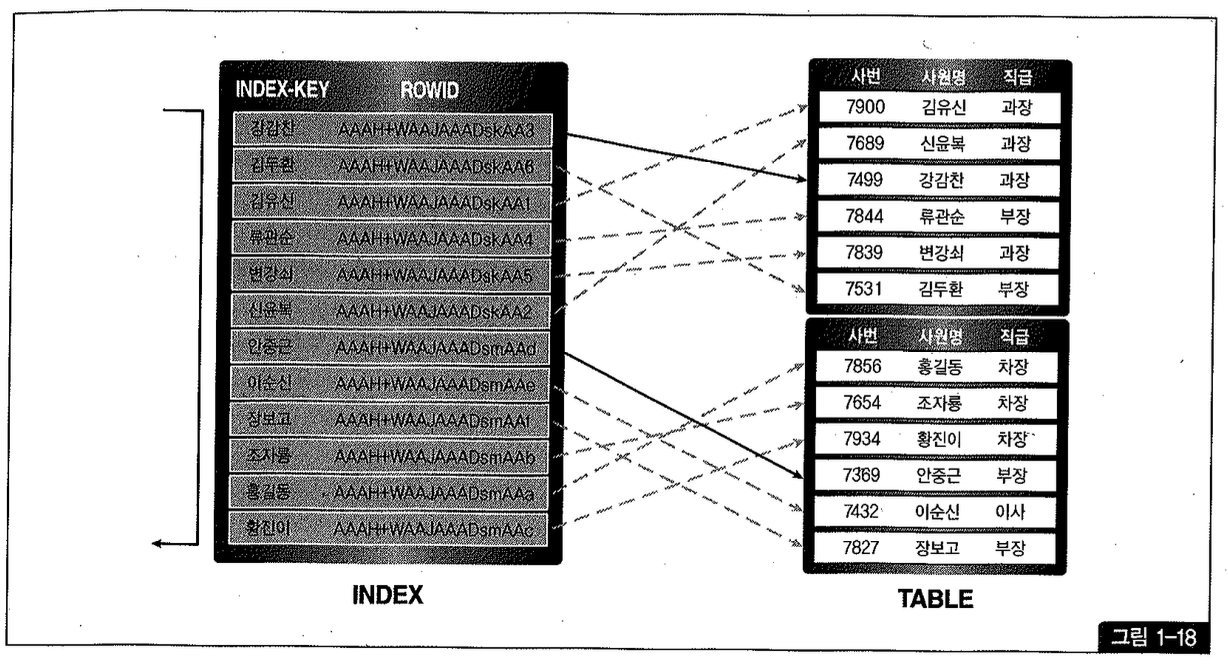
그림 1-18을 보면서 세부적인 작동원리를 이해해 보자.

그림 1-18은 사원명 인덱스에서 12개 로우를 스캔하면서 건건이 테이블을 액세스하는 과정을 화살표로 표현하고 있다. 굵은 실선은 해시 체인 래치를 획득한 후 블록을 액세스하는 것을 의미하고, 흐린 점선은 래치 획득 없이 버퍼를 Pin한 상태에서 액세스하는 것을 의미한다.

예를 들어, 두 번째 인덱스 레코드 ‘김두한’을 위해 테이블 블록을 읽을 때는 앞서 ‘강감찬’ 레코드를 위해 읽었던 첫 번째 테이블 블록을 Pin한 상태에서 액세스하기 때문에 논리적인 블록 I/O를 일으키지 않는다.

여섯 번째 ‘신윤복’까지 같은 방식으로 읽다가 ‘안중근’ 레코드에도 달해서야 다른 테이블 블록을 가리키는 것이 확인된다. 이때 비로소 래치를 얻어 새로운 블록을 읽는다. 그러고 나서 나머지 다섯 개 레코드도 같은 블록을 가리키므로 버퍼 Pinning 상태에서 가볍게 액세스한다.

이처럼 CF가 좋을 때는(완전히 같은 순서로 정렬돼 있을 필요는 없으며, 그림1-18에서 보듯 같은 테이블 블록에 모여 있기만 하면 됨) 인덱스를 통해 12개의 테이블 레코드를 읽는데 Random 블록 I/O가 단 2회만 발생한다.

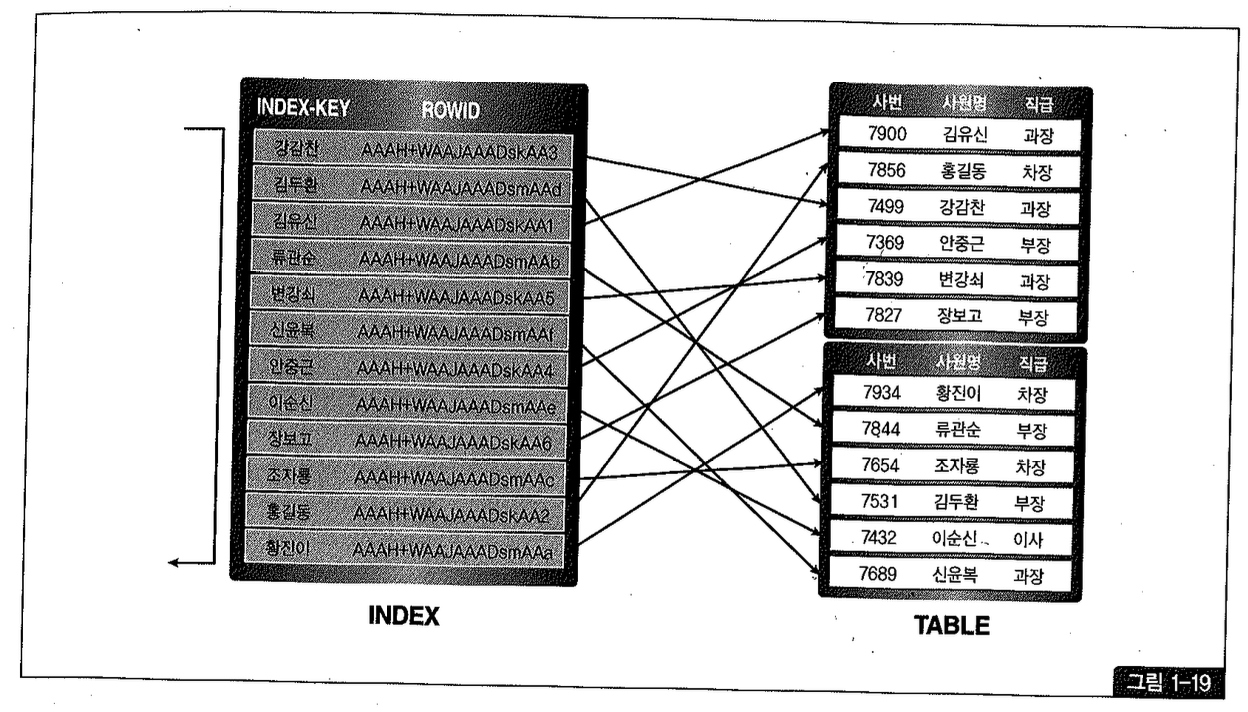
그림 1-19를 보면 모든 화살표가 굵은 실선인 것을 볼 수 있다. 똑같이 12개의 사원 레코드를 인덱스를 통해 읽는데 매번 해시 체인 래치 획득 과정을 거쳐 무겁게 논리적 블록 읽기를 수행함을 표현한 것이다.

그림 1-19처럼 CF가 나쁘면 최악에는 12개 레코드를 읽기 위해 Random 블록 IVO가 12번 발생한다.

버퍼 Pinning 효과를 이용하거나 인위적으로 클러스터링 팩터를 높게 만들어 튜닝하는 사례를 다음 절 후반부에 소개하므로 참조하기 바란다.

(3) 인덱스 손익분기점

앞에서 설명한 것처럼 인덱스 rowid에 의한 테이블 액세스는 생각보다 고표시능 구조이고, 따라서 일정량을 넘는 순간 테이블 전체를 스캔할 때보다 오히려 더 느려진다. Index Range Scan에 의한 테이블 액세스가 table Full Scan보다 느려지는 지점을 흔히 손익분기점이라고 부른다.

인덱스에 의한 액세스가 Full Table Scan보다 더 느려지게 만드는 가장 핵심적인 두 가지 요인은 다음과 같다.

• 인덱스 rowid에 의한 테이블 액세스는 Random 액세스인 반면, Full Table Scan은 Sequential 액세스 방식으로 이루어진다. • 디스크 I/O 시, 인덱스 rowid에 의한 테이블 액세스는 Single Block Read 방식을 사용하는 반면, Full Table Scan은 Multiblock Read 방식을 사용한다.

이런 요인에 의해 인덱스 손익분기점은 일반적으로 5~20%의 낮은 수준에서 결정되지만 CF에 따라 크게 달라진다. 인덱스의 CR이 나쁘면 같은 테이블 블록을 여러 번 반복 액세스하면서 논리적 I/O 개수가 증가하고 물리적 I/O 발생량도 증가하기 때문이다. 따라서 CF가 나쁘면 손익분기점은 5% 미만에서 결정되며, 심할 때는 (BCHR가 매우 안 좋을 때) 1% 미만으로 떨어진다. 반대로 OF가 아주 좋을 때는 손익분기점이 90% 수준까지 올라가기도 한다.

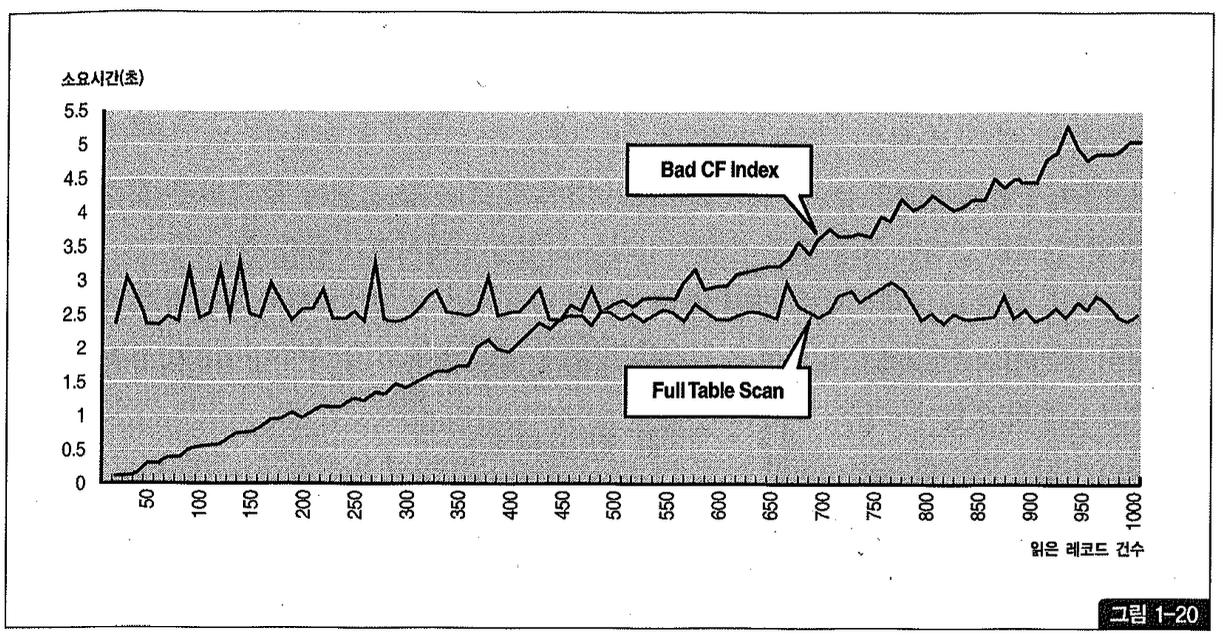
CF가 가장 안 좋은(= 총 레코드 개수에 근접) 인덱스를 이용하니까 그림 1-20에서 보는 것처럼 0.5% 수준에서 손익분기점이 결정되는 것을 볼 수 있다. 즉, 100,00개 레코드 중에서 50개 레코드를 넘는 순간 이미 Full Table Scan에 비해 인덱스 스캔이 더 느려졌다. (‘읽은 레코드 건수’는 1,00건까지만 표시했다.)

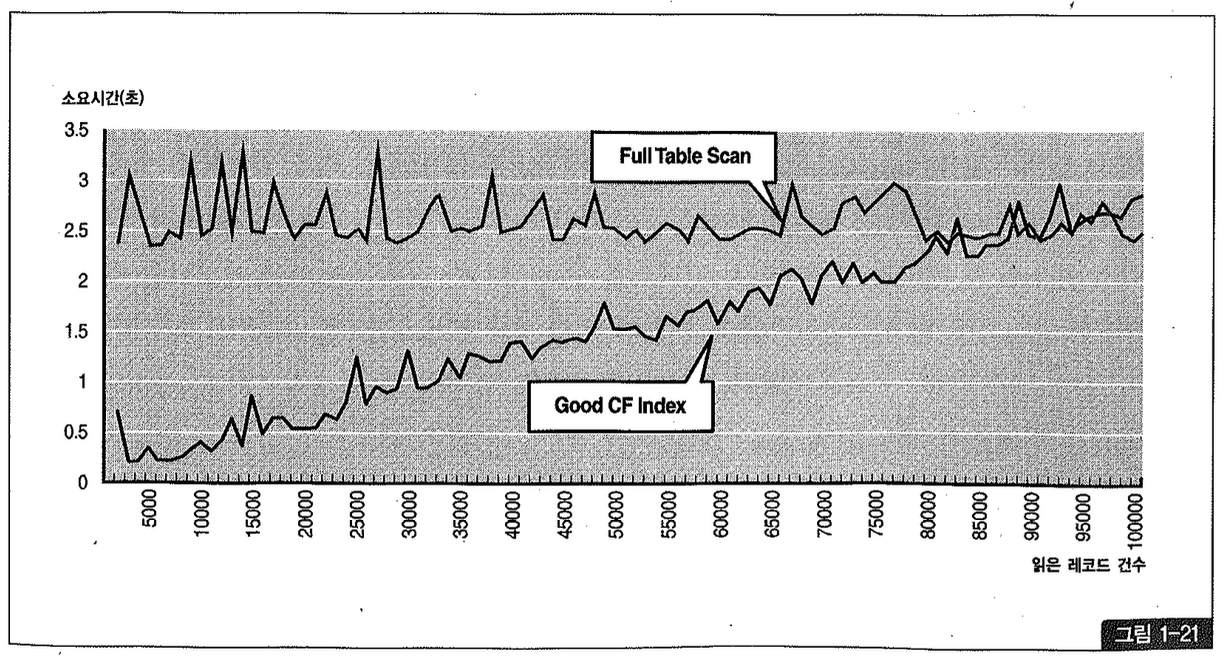
CH가 가장 좋은(= 총 블록 개수에 근접) 인덱스를 이용하는 경우는 어떨까? 그림 1-21에서 보는 것처럼 100,000개 레코드 중 95,000개 레코드를 넘는 순간에 이르러서야 Full Table Scan 보다 느려졌으므로, 손익분기점은 95% 수준에서 결정되었다.

그림 1-20과 1-21에서 보듯이, Full Table Scan 할 때는 CP에 상관없이 양쪽 모두 평균 2.5~3 초 수준에 머무른다는 사실을 확인하기 바란다.

방금 보았듯이 인덱스 손익분기점은 데이터 상황에 따라 크게 달라지므로 5%, 10%, 20%처럼 정해진 수치 또는 범위를 정해놓고 인덱스의 효용성을 판단하면 틀리기 쉽다.

오해하지 말 것은, 손익분기점은 인덱스가 항상 좋을 수 없음을 설명하려고 도입한 개념일뿐 이를 높이기 위해 어떤 조치를 취하라는 것은 아니다. 즉, 테이블 스캔이 항상 나쁜 것은 아니며 바꿔 말해, 인덱스 스캔이 항상 좋은 것도 아니라는 사실을 인식시키기 위함이다.

물론 테이블을 Reong 함으로써 CF를 좋게 만든다면 인덱스 손익분기점이 높아져 그 인덱스의 효용성이 증가하지만 실사례를 다음 절에서 소개함), 그런 방안은 최후의 수단이어야지 일상적인 튜닝 기법으로 남용하지 말아야 한다.

인덱스가 갖는 한계를 극복하려면 바로 이어서 설명할 DBMS 제공 기능들을 이용하거나 1권 5장에서 설명한 부분 범위 처리 원리를 적극 활용해야 한다. 인덱스 스캔 비효율이 없도록 잘 구성된 인덱스를 이용해 부분 범위 처리 방식으로 프로그램을 구현한다면 그 인덱스의 효용성은 100%가 된다. 무조건 인덱스를 사용하는 쪽이 유리하다는 것이다.

손익분기점을 극복하기 위한 기능들

손익분기점 원리에 따르면 선택도가 높은 인덱스는 효용가치가 낮지만 대용량 테이블을 Full Scan하는 것 역시 비효율이 크다. 그럴 때 오라클이 제공하는 기능들을 잘 활용하면 인덱스의 손익분기점 한계를 극복할 수 있다.

첫 번째 기능은 IOT(인덱스 조직화 테이블)로서, 테이블을 인덱스 구조로 생성하는 것을 말한다. 테이블 자체가 인덱스 구조이므로 항상 정렬된 상태를 유지한다. 그리고 인덱스 리프 블록이 곧 데이터 블록이어서 인덱스를 수직 탐색한 다음에 테이블 레코드를 읽기 위한 추가적인 Random 액세스가 불필요하다. IOT에 대한 자세한 설명은 6절을 참조하기 바란다.

두 번째는 클러스터 테이블(Clustered Table)이다. 키 값이 같은 레코드는 같은 블록에 모이도록 저장하기 때문에 클러스터 인덱스를 이용할 때는 테이블 Random 액세스가 키 값별로 한 번씩만 발생한다. 클러스터에 도달해서는 Sequential 방식으로 스캔하기 때문에 넓은 범위를 읽더라도 비효율이 없다. 클러스터에 대한 자세한 설명도 6절을 참조하기 바란다.

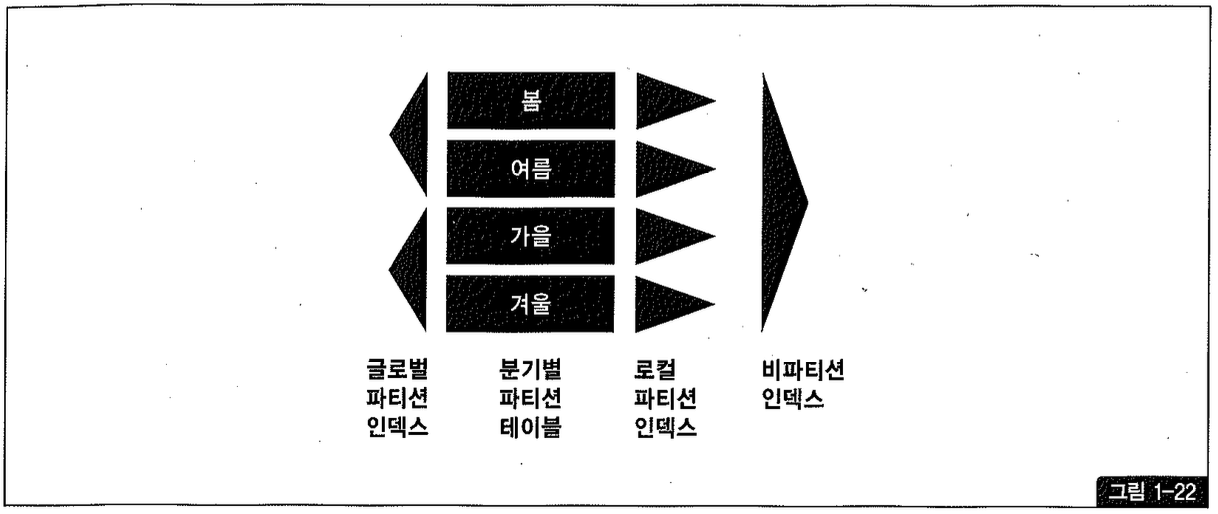
인덱스 손익분기점을 극복하기 위한 세 번째 기능은 파티셔닝이다. 읽고자 하는 데이터가 많을 때는 인덱스를 이용하지 않는 편이 낫다고 하지만, 수천만 건에 이르는 테이블을 Full Scan해야 한다면 난감하기 그지없다. 그럴 때, 대량 범위 조건으로 자주 사용되는 컬럼 기준으로 테이블을 파티셔닝한다면 Full Table Scan 하더라도 일부 파티션만 읽고 멈추도록 할 수 있다.

클러스터는 기준 키 값이 같은 레코드를 블록 단위로 모아놓지만 파티셔닝은 세그먼트 단위로 모아놓는 점이 다르다. 그림 1-22를 참고하기 바라고, 자세한 내용은 6장에서 설명한다.