Post

<오라클 성능 고도화 원리와 해법2> Ch02-05 Outer 조인

Posted Updated
By Mijong Go 21 min read

오라클 성능 고도화 원리와 해법2 - Ch02-05 Outer 조인

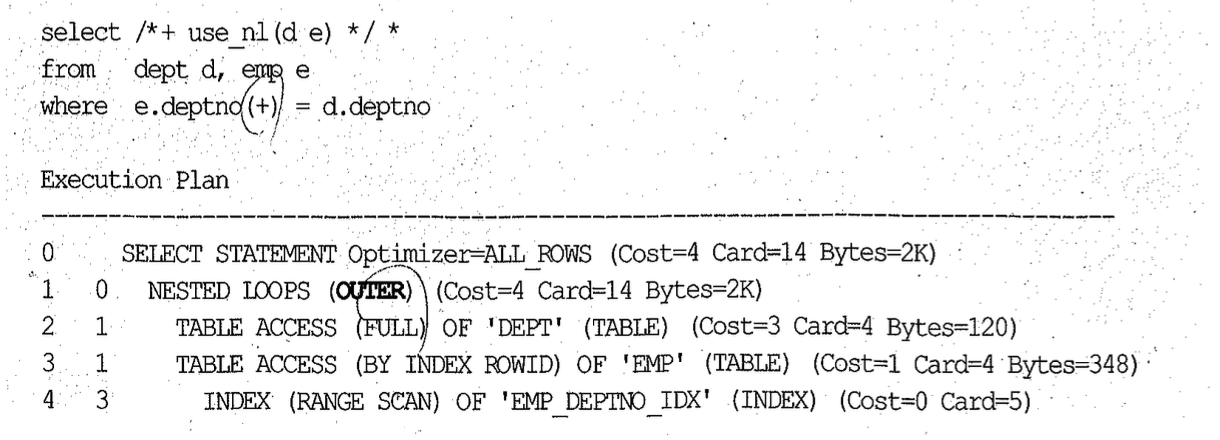
(1) Outer NL 조인

NL 조인은 그 특성상 Outer 조인할 때 방향이 한쪽으로 고정되며, Outer 기호(+)가 붙지 않은 테이블이 항상 드라이빙 테이블로 선택된다. leading 힌트를 이용해 순서를 바꿔보려 해도 소용 없다.

4절에서 보았듯이 NL 조인이 조인 순서에 가장 큰 영향을 받는다. 조인 순서 때문에 성능이나 빠지지 않게 하려면 불필요한 Outer 조인이 발생하지 않도록 주의해야 한다.

ERD 표기를 따르는 SQL 개발의 중요성

데이터베이스 프로그래머에게는 BRD 표기법에 대한 정확한 이해가 필수적이다. BIRD를 잘못 해석하면 설계 의도와 다른 데이터를 발생시킬 수 있기 때문이며, 이는 여닫이문으로 설계된 도면을 보고 미닫이문으로 시공하는 것이다. SQL을 작성할 때는 각 속성의 Null 값 허용 여부를 반드시 확인해야 하고, 엔티티 간 관계(relationship)를 해석할 때에도 카디널리티(Crow’s foot, 1:1, M:N 등) 만 보지 말고 Optionality를 반드시 따져봐야 한다.

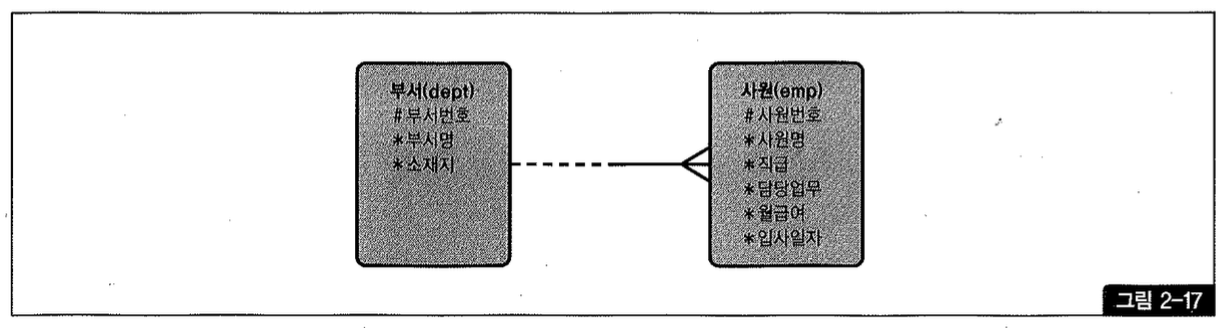
설계 의도를 잘못 해석하면 데이터 품질뿐만 아니라 쿼리 성능에도 영향을 미칠 수 있다. 예를 들어, 그림2-17에서는 사원이 전혀 없는 유령 부서(또는 아직 부서원이 배정되지 않은 신규 부서)가 등록될 수 있다(부서 쪽 관계선이 점선). 따라서 사원 유무와 상관없이 모든 부서가 출력되도록 하려면 사원 쪽 모든 조건절에 Outer 기호(+)를 반드시 붙여줘야 한다.

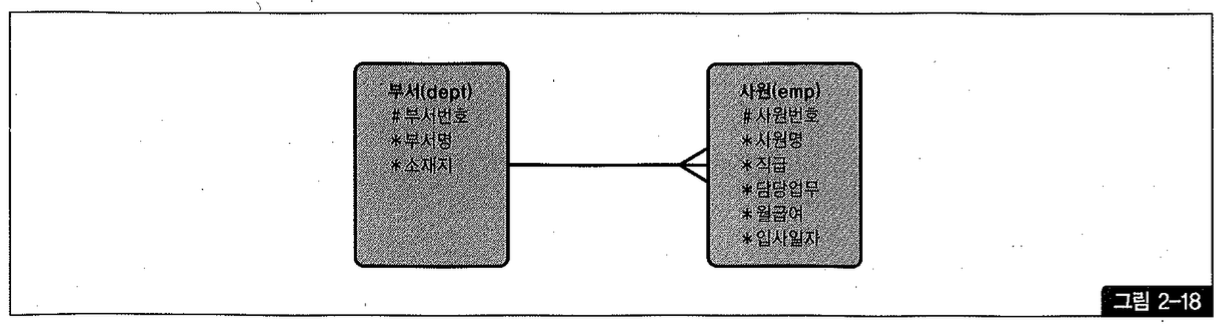
하지만 그림2-18에서는 사원 없는 부서가 등록될 수 없다(부서 쪽 관계선이 실선). 따라서 모든 부서가 출력되도록 하려고 굳이 Outer 조인할 필요가 없음에도 Outer 기호(+)를 붙인다면 성능이 나빠질 수 있는 것이다.

그리고 그림 2-17과 2-18 모두 사원 쪽 부서 번호가 필수(Mandatory) 컬럼이다. 즉, 소속 부서 없는 사원이 존재할 수 없다는 뜻이므로 테이블을 생성할 때 Not Null 제약을 두어야 한다. DBMS에 실제 Not Null 제약을 생성했건 안했건 그 컬럼에 Null 값이 들어올 수 없도록 하려는 것이 설계자의 의도이므로 프로그램도 그에 맞게 개발해야 한다.

  1. ERD 상에 표시된 설계자의 의도를 무시하고 테이블 생성시 Not Null 제약을 두지 않는 경우를 종종 보는데, 결코 바람직한 현상이 아니다. 데이터 품질이 중요하다는 것이 첫번째 이유고, 옵티마이저에게 매우 중요한 정보로서 성능에도 영향을 준다는 것이 두번째 이유다.

따라서 사원을 기준으로 부서 테이블과 Outer 조인 하는 것은 불 필 요 하 며, 만 약 Inner 조 인 을 했을 때 걸러지는 사원 레코드가 있다면 조회 프로그램이 아니라 입력/수정/삭제 프로그램을 고쳐야할 일이다. 물론 데이터 정제(cleansing) 작업도 함께 실시해야 한다. 그런데도 혹시 있을지 모를 Null 값을 두려워해 습관적으로 Outer 기호(+)를 붙인다면 성능상 불이익이 생길 수 있음을 명심하기 바란다.

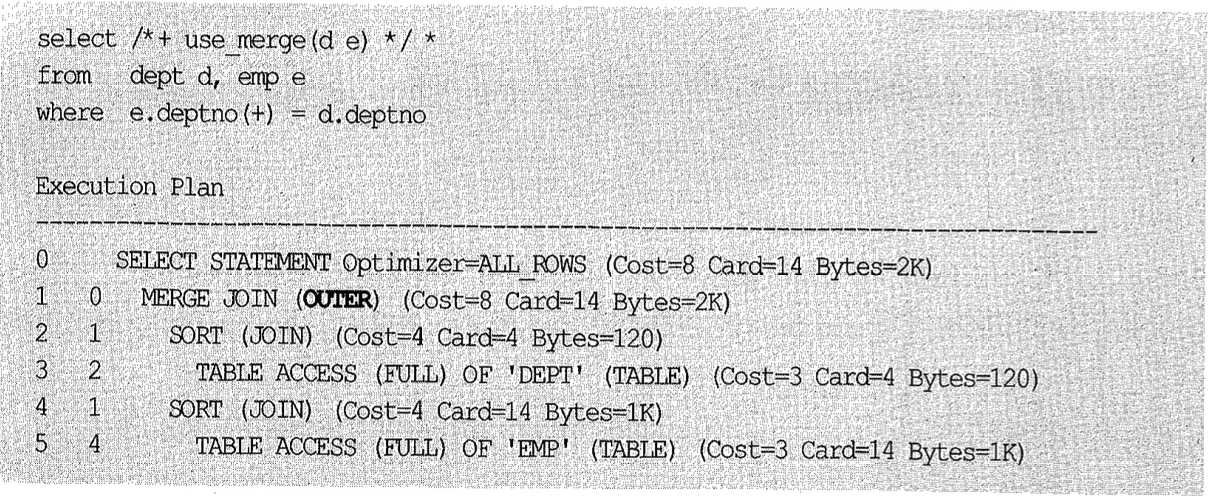
(2) Outer 소트머지조인

소트머지조인은 소트된 중간 집합을 이용한다는 점만 다를 뿐 처리 루틴이 NL 조인과 다르지 않다고 했다. 따라서 Outer 소트머지조인도 처리 방향이 한쪽으로 고정되며, Outer 기호(+)가 붙지 않은 테이블(Outer 테이블)이 항상 First 테이블로 선택된다. leading 힌트를 이용해 순서를 바꿔보려 해도 소용 없다.

(3) Outer 해시조인

Outer 해시조인도 9i까지는 방향이 고정됐었다. 91에서 Outer 해시조인을 수행해보면, Outer 기호(+)가 붙지 않은 테이블(outer 테이블)이 항상 BuildInput으로 선택된다.

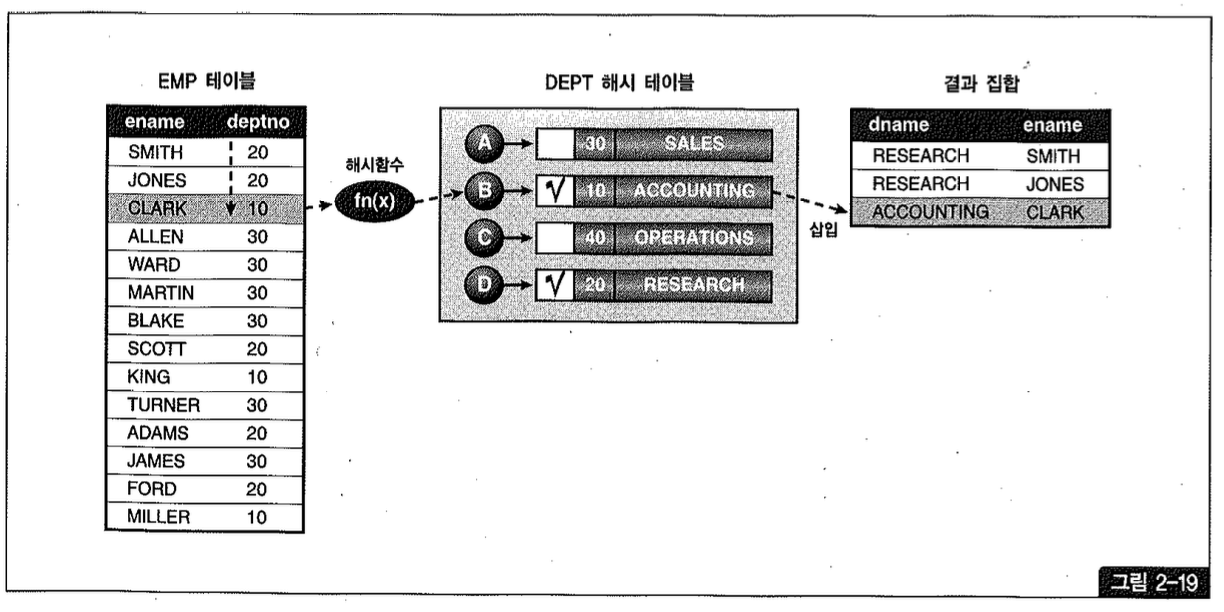
실행 계획이 위와 같을 때 오라클은 아래와 같은 알고리즘을 사용해 Outer 해시조인을 처리한다.

  1. Outer 집합인 dept 테이블을 해시 테이블로 빌드(Build)한다.
  2. Inner 집합인 cmp 테이블을 읽으면서 해시 테이블을 탐색(Probe)한다.
  3. 조인에 성공한 레코드는 곧바로 결과 집합에 삽입하고, 조인에 성공했음을 해시 엔트리에 표시해 둔다(그림2-19).
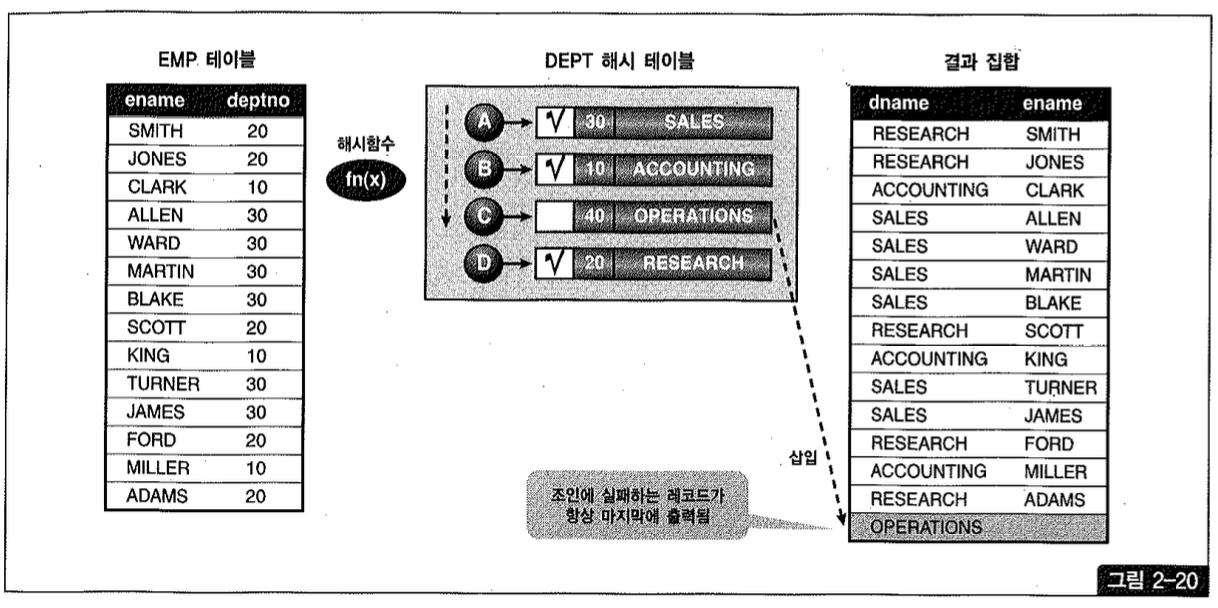
  4. Probe 단계가 끝나면 Inner 조인과 동일한 결과 집합이 만들어진 상태다. 이제 조인에 실패했던 레코드를 결과 집합에 포함시켜야 하므로 해시 테이블을 스캔(PGA에서 스캔하므로 비용이 매우 낮음)하면서 체크가 없는 dept 엔트리를 결과 집합에 삽입한다(그림2-20), 그럼으로써 Outer 조인을 완성한다.

해시조인은 특히 대용량 테이블을 조인할 때 자주 사용되는데, Outer 조인할 때 이처럼 조인 순서가 고정되다 보니 자주 성능 문제를 일으켰다. 예를 들어, 주문 테이블을 기준으로 고객 테이블과 Outer 조인하는 경우에 대용량 주문 테이블을 해시 테이블로 빌드해야 하는 문제가 생긴다. Hash Area가 부족해 디스크 쓰기와 읽기가 발생할 뿐만 아니라 주문 건수가 많은 고객일수록 해시 버킷당 엔트리 개수가 많아져 해시 테이블을 탐색하는 효율이 크게 저하된다. 이 두 가지 요인에 의해 해시조인 성능이 얼마나 나빠지는지는 3절에서 충분히 설명하였다.

오라클은 이 문제를 해결하려고 10g에서 아래와 같은 Right Outer 해시조인을 도입하게 되었다.

실행 계획이 위와 같을 때 오라클은 아래와 같은 알고리즘을 사용해 Outer 해시조인을 처리한다.

  1. Inner 집합인 dept 테이블을 해시 테이블로 빌드(Build)한다.
  2. Outer 집합인 emp 테이블을 읽으면서 해시 테이블을 탐색(Probe)한다.
  3. Outer 조인이므로 조인 성공 여부에 상관없이 결과 집합에 삽입한다.

이미 느꼈겠지만 Right Outer 해시조인은 결국 Outer NL 조인과 같은 알고리즘을 사용한다. Outer 해시조인을 애초에 이런 방식으로 처리할 수 있었을 텐데 오라클은 왜 10g에 와서야 이 방식을 추가로 도입한 것일까?

Right Outer 해시조인 탄생 배경

일반적으로 Outer 조인은 1쪽 집합을 기준으로 하는 경우가 많다. 예를 들면, 그림2-21에서 고객을 기준으로 주문과 Outer 조인하거나 상품을 기준으로 주문과 Outer 조인하는 경우다. 모델상에서 보면 주문 기준으로 고객 또는 상품과 Outer 조인할 이유는 없다. ‘고객 없는 주문’ 또는 ‘상품 없는 주문’을 허용하지 않도록 설계돼있기 때문이다.

오라클은 이런 사실을 감안해 Outer 테이블을 해시 테이블로 빌드하는 알고리즘을 애초에 선택하였다. Inner 조인하고 나서 해시 테이블을 전체적으로 한 번 더 스캔하는 비효율을 감수하면서까지 말이다. 이유는, 작은 쪽 집합을 해시 테이블로 빌드하는 게 유리하기 때문이다.

그런데 그림2-21과 같은 일반적인 엔티티 관계(relationship) 속에서도 주문을 기준으로 고객 또는 상품과 Outer 조인해야 할 필요성이 생긴다. 모델상으로는 부모 없는 자식 레코드가 있어선 안 되지만(FK를 설정하지 않은 채 DBMS를 운영하는 경우가 많다 보니 실제 그런 레코드들이 많이 생긴다. 그럼2-22 같은 상태가 되는 것이다.

프로그램 버그일 수도 있고, 활동성 없는 고객이나 오래된 상품 레코드를 지우면서 관련된 자식 레코드(주문 등)는 지우지 않아 생기는 현상이다. 데이터 정제(Cleansing) 작업할 때 M쪽 자식 테이블을 기준으로 Outer 조인하는 쿼리가 자주 사용되는 이유다.

그럴 때 주문 같은 초대용량 테이블을 해시 테이블로 생성해야 하기 때문에 성능이 여간 나쁘지 않은데, 정제 작업이 많은 데이터 이행(migration) 업무를 해본 독자라면 깊이 공감할 것이다.

‘고객 없는 주문’, ‘상품 없는 주문’이 발견됐을 때 이를 정제하지 않고 데이터를 그대로 이행하는 경우도 많다. 중요한 주문 데이터를 지우면 그와 관련된 각종 집계값들이 안 맞을 수 있어 업무 담당자 입장에서도 쉽게 결정을 내리지 못하기 때문이다. 그러다 보니 주문을 기준으로 고객과 상품 테이블을 Outer 조인한 결과를 신시스템에 그대로(정합성이 안 맞더라도) 이행하는 경우가 생기고, 그런 작업을 담당한 개발자는 성능 때문에 곤혹스런 상황에 부닥치게 된다.

이런 성능 이슈를 해결하려고 오라클은 10g부터 Inner 쪽 집합을 해시 테이블로 빌드할 수 있는 알고리즘을 추가하게 되었다.

9i 이전 버전에서 Outer 해시조인 튜닝

그럼 Right Outer 해시조인이 도입되기 전 9i까지는 위와 같은 상황에서 어떻게 튜닝할 수 있을까?

1
2
3
4
5
6
7
8
9

SELECT /*+ ordered indexffs(o) full(e) full(02) use hash(o c) usehash(02)
          parallel_index(o) parallel(c) parallel(02) */
       c.*,
       o2.*
FROM 주문 o, 고객 c, 주문 o2
WHERE c.고객번호(+) = o.고객번호
  AND o2.고객번호 - o.고객번호
  AND o2.상품번호 - o.상품번호
  AND o2.주문일시 - o.주문일시;

위 쿼리를 보면, 처음 주문(O)과 고객(c) 테이블을 Outer 조인할 때는 주문 테이블에서 PK 인덱스만 빠르게 읽어 Outer 조인을 완성하고, 주문(O2) 테이블과 다시 한 번 조인하면서는 Inner 조인하도록 했다. 주문이 워낙 대용량이어서 인덱스 블록만 읽더라도 In-Memory 해시조인은 불가능하겠지만 Build Input 크기를 줄임으로써 디스크 쓰기 및 읽기 작업을 최소화하려는 아이디어다.

하지만 이 방법은 디스크 쓰기와 읽기 작업을 줄여주는 효과는 있지만 해시 버킷당 엔트리 개수가 많아서 생기는 문제는 피할 수가 없다.

만약 이 때문에 조인 성능이 느리다면 주문 일시 구간을 나눠 쿼리를 여러 번 수행하는 방법을 생각해볼 수 있다. 주문 테이블은 주문 일시로 Range 파티셔닝돼 있을 것이고, 일정한 주문 일시 구간 내에서의 고객별 주문 건수는 많지 않을 것이기 때문에 해시 버킷당 엔트리 개수를 최소화할 수 있다. 그러면 고객 테이블을 반복적으로 읽는 비효율에도 불구하고 더 빠르게 수행될 것이다.

(4) Full Outer 조인

테스트를 위해 우선 ‘입금’과 ‘출금’ 테이블을 아래와 같이 생성해보자(스크립트 ch2_08.txt 참조).

Left Outer 조인 + Union All + Anti 조인(Not Exists 필터) 이용

입금과 출금, 두 테이블을 Full Outer 조인해서 고객 별 입금 액과 출금 액을 같이 집계하려고 한다. 이를 위해 가장 일반적으로 사용할 수 있는 방법은 다음과 같다.

ANSI Full Outer 조인

위와 같이 쿼리를 복잡하게 작성하지 않고도 Full Outer 조인할 수 있도록 오라클 9i부터 아래와 같이 ANSI 구문을 지원하기 시작했다.

그런데 위 실행 계획을 보면 내부적으로는 Left Outer 조인 + Union All + Anti 조인(Not Exists) 방식을 그대로 사용하고 있다. 쿼리가 간단해졌을 뿐 입금과 출금 테이블을 각각 두 번 씩 액세스하는 비효율은 그대로 안고 있다.

Native Hash Full Outer 조인

이에 오라클 11g에서 Native Hash Full Outer 조인을 선보였고, 필요하면 10.2.0.4 버전에서도 Hidden 파라미터 optimizer_nativefullouterjoin를 조정해 이 기능을 사용할 수 있다.

실행 계획을 보면, 입금과 출금 테이블을 각각 한 번씩만 액세스한다는 것이 가장 큰 변화다. 입금액이 Null인 레코드가 마지막에 출력된 것을 통해, 내부적으로 어떤 식으로 처리하는지 추정할 수 있다.

  1. 출금 테이블을 해시 테이블로 빌드(Build)한다.
  2. 입금 테이블로 해시 테이블을 탐색(Probe)하면서 조인한다.
  3. 조인 성공 여부에 상관없이 결과 집합에 삽입하고, 조인에 성공한 출금 레코드에는 체크 표시를 해둔다(그림2-19 참조).
  4. Probe 단계가 끝나면 Right Outer 해시 조인한 것과 동일한 결과 집합이 만들어진다. 이제 해시 테이블을 스캔하면서 체크 표시가 없는 출금 레코드를 결과 집합에 삽입(그림2-20 참조)함으로써 Full Outer 조인을 완성한다. 입금액이 Null인 레코드가 마지막에 출력된 이유가 바로 이것이다.

Union All을 이용한 Full Outer 조인

아래와 같이 union all을 이용하면 버전에 상관없이 Full Outer 조인된 결과 집합을 얻을 수 있다. 두 테이블을 각각 한 번씩만 액세스하였으며, 조인 대신 Sort(또는 hash) group by 연산을 수행한다.

Database, SQL Tuning
SQLP
This post is licensed under CC BY 4.0 by the author.