<오라클 성능 고도화 원리와 해법2> Ch03-06 히스토그램

Posted May 2, 2024

By Mijong Go 16 min read

오라클 성능 고도화 원리와 해법2 - Ch03-06 히스토그램

(1) 히스토그램 유형

지금까지는 히스토그램이 없는 상황에서 옵티마이저가 선택도와 카디널리티를 구하는 원리를 주로 설명하였는데, 히스토그램이 있으면 더 정확한 카디널리티를 구할 수 있다. 특히, 분포가 균일하지 않은 컬럼으로 조회할 때 효과를 발휘한다.

오라클이 사용하는 히스토그램으로는 아래 두 가지 유형이 있다.

높이 균형(Height-Balanced) 히스토그램
도수 분포(Frequency) 히스토그램

히스토그램을 생성하려면 컬럼 통계 수집 시 버킷 개수를 2 이상으로 지정 (예: for columns SIZE 10 col, co, co3) 하면 된다.

히스토그램 정보는 dba_histograms 또는 dba_tab_histograms 뷰를 통해 확인할 수 있다. 특히, 10g에서는 dba_tab_columns 뷰에 histogram 컬럼이 추가되면서 히스토그램 유형을 쉽게 파악할 수 있게 되었다. 아래는 이 컬럼에 표시되는 값에 대한 설명이다.

FREQUENCY: 값 별로 빈도수를 저장하는 도수 분포 히스토그램 (값의 수 = 버킷 개수)
HEIGHT-BALANCED: 각 버킷의 높이가 동일한 높이 균형 히스토그램 (값의 수 = 버킷 개수)
NONE: 히스토그램을 생성하지 않은 경우

(2) 도수 분포 히스토그램

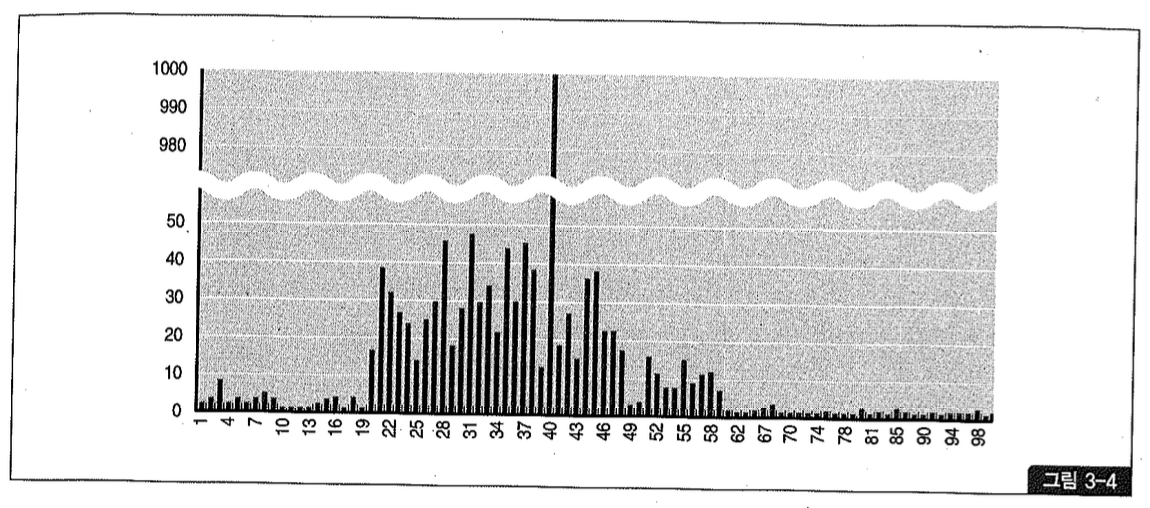
‘value-based 히스토그램’으로도 불리며, 그림3-4처럼 값 별로 빈도수 (frequency number) 를 저장하는 히스토그램을 말한다.

도수 분포 (frequency) 히스토그램은 컬럼 값마다 하나의 버킷을 할당 (값의 수 = 버킷 개수) 한다. 사용자가 요청한 버킷 개수가 컬럼이 가진 값의 수보다 많거나 같을 때 사용되며, 최대 254개의 버킷 만 허용하므로 값의 수가 254개를 넘는 컬럼에는 이 히스토그램을 사용할 수 없다.

쿼리 결과에서 보듯, 도수 분포 히스토그램에서는 컬럼 값의 수 (INDV, number of distinct values) 와 버킷 개수가 항상 일치한다. 컬럼 값마다 단일 버킷을 할당하기 때문이다.

그리고 100개의 버킷을 요청했는데 89개만 생성된 것은 실제 값의 종류가 89개뿐이기 때문이다. 254개를 요청하더라도 값의 수만큼만 버킷을 할당하므로 정확한 히스토그램을 위해서라면 항상 254개를 요청하는 것이 좋다.

히스토그램 정보를 조회 할 수 있는 dba/all/user_histograms 뷰에는 아래 두 컬럼이 있다.

endpoint_value: 버킷에 할당된 컬럼 값
endpoint_number: endpoint_value로 정렬했을 때, 최소 값부터 현재 값까지의 누적 수량

endpoint_number가 누적 수량을 의미하므로 바로 앞 endpoint_value 까지의 누적 수량을 차감 함으로써 해당 버킷의 값 빈도수를 알 수 있다.

도수 분포 히스토그램은 값 별로 빈도수를 미리 계산해두는 방식이기 때문에 조건절을 만족하는 카디널리티를 쉽고 정확하게 구할 수 있다 (하지만, 시스템 자원에 한계가 있으므로 100만 고객명을 도수 분포 히스토그램으로 관리하는 경우를 상해보래) 컬럼 값의 빈도수를 모두 이런 식으로 저장할 수는 없다. 그래서 값의 수가 많을 때는 높이 균형 히스토그램을 사용한다.

(3) 높이 균형 히스토그램

‘equi-depth 히스토그램’ 으로도 불린다. 컬럼이 가진 값의 수보다 적은 버킷을 요청할 때 만들어진다. 높이 균형(heighi-balanced) 히스토그램에서는 버킷 개수보다 값의 수가 많기 때문에 하나의 버킷이 여러 개 값을 담당한다. 예를 들어, 값의 수가 100개인데 10개의 버킷을 요청하면 하나의 버킷이 평균적으로 10개의 값을 대표한다. 요청할 수 있는 최대 버킷 개수는 254개이므로 값의 수가 254 개를 넘으면 무조건 이 히스토그램이 만들어진다.

높이 균형 히스토그램에서는 말 그대로 각 버킷의 높이가 같다. 각 버킷은 (L/(버킷 개수) X 100)의 데이터 분포를 갖는다. 따라서 각 버킷(~값이 아니라 버킷)이 갖는 빈도수는 (총 레코드 개수)/(버킷 개수) 로써 구할 수 있다.

popular value에 대한 선택도/카디널리티 계산

조건절 값이 두 개 이상 버킷을 가진 popular value이면 아래 공식을 따른다.

선택도 = (조건값의 버킷 개수)/(총 버킷 개수)

즉, 조건값의 버킷 개수가 총 버킷 개수(히스토그램 뷰에서 조회되는 가장 큰 endpoint number 값)에서 차지하는 비중을 가지고 선택도를 구한다. 예제 데이터에서 popular value 40은 총 20개 버킷 중 10개를 사용하므로 선택도는 1/2 = 50% 이다.

카디널리티 = 총 레코드 수 x 선택도
        = (총 레코드 수) X (조건값의 버킷 개수)/(총 버킷 개수)
        = 2,000 x 10 / 20 = 1,000

non-popular value에 대한 선택도/카디널리티 계산

non-popular value일 때는 미리 구해놓은 density 값을 이용한다.

카디널리티 = 총 레코드 수 x 선택도 = 총 레코드 수 x density

density가 0.2567285이므로 총 레코드 수 2,000을 곱한 카디널리티는 513이다. 실제 non-popular value를 조회하는 조건에 대한 실행 계획을 보면, 아래와 같이 Rows가 513으로 구해지는 것을 확인할 수 있다.

SQL> select * from member where age - 39;

density
컬럼 통계를 보면 density 값이 있는데, 해당 컬럼을 조건으로 검색할 때의 선택도를 미리 구해놓은 값으로 이해하면 된다. 히스토그램이 없거나, 있더라도 100% 균일한 분포를 갖는다면 density 값은 항상 1/num_distinct와 일치하지만 그렇지 않은 상황에서는 다른 값을 가질 수도 있다. 복잡한데다 꼭 알아야 하는 내용도 아니므로 굳이 공식을 이해하려고 노력할 필요는 없다. 다만, ‘=’ 조건 조회 시 옵티마이저가 어떤 때는 1/num_distinct를 이용하고 어떤 때는 미리 구해놓은 density 값을 이용한다는 사실만큼은 기억할 필요가 있다.

density

컬럼 통계를 보면 density 값이 있는데, 해당 컬럼을 조건으로 검색할 때의 선택도를 미리 구해놓은 값으로 이해하면 된다. 히스토그램이 없거나, 있더라도 100% 균일한 분포를 갖는다면 density 값은 항상 1/num_distinct와 일치하지만 그렇지 않은 상황에서는 다른 값을 가질 수도 있다.

복잡한데다 꼭 알아야 하는 내용도 아니므로 굳이 공식을 이해하려고 노력할 필요는 없다. 다만, ‘=’ 조건 조회 시 옵티마이저가 어떤 때는 1/num_distinct를 이용하고 어떤 때는 미리 구해놓은 density 값을 이용한다는 사실만큼은 기억할 필요가 있다.

(4) 바인드 변수 사용 시 카디널리티 계산

바인드 변수를 사용하면, 최초 수행할 때 최적화를 거친 실행 계획을 캐시에 적재하고 실행 시점에는 그것을 그대로 가져와 값만 다르게 바인딩하면서 반복 재사용하게 된다. 여기서, 변수를 바인딩하는 시점이(최적화 시점보다 나중인) 실행 시점이라는 사실이 중요하다. 즉, SQL을 최적화하는 시점에 조건절 컬럼의 데이터 분포를 활용하지 못하는 문제점을 갖는다. (“바인드 변수를 사용하면 통계 정보를 사용하지 못한다”고 흔히 말하는데, 정확히 표현하면 컬럼 히스토그램 정보를 사용하지 못하는 것이다. 히스토그램을 제외한 다른 통계 정보들은 충분히 활용한다.)

따라서 바인드 변수를 사용할 때 옵티마이저는 평균 분포를 가정한 실행 계획을 생성한다. 컬럼 분포가 균일할 때는 문제될 것이 없지만 그렇지 않을 때는 실행 시점에 바인딩되는 값에 따라 최적이 아닌 실행 계획일 수 있어 문제다. 특히 부등호, Between 같은 범위 검색 조건을 사용할 때가 문제인데, 먼저 조건인 경우부터 살펴보자.

’=’ 조건일 때

바인드 변수로 검색할 때 선택도는 아래와 같이 구해진다.

히스토그램이 없을 때: 1/num_distinct 사용
도수 분포 히스토그램일 때: 1/num_distinct 사용
높이 균형 히스토그램일 때: density 사용

범위 검색 조건일 때

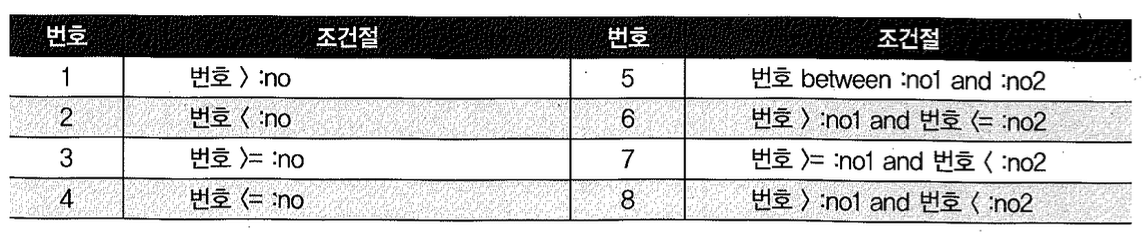
범위 검색 조건이 사용되면 옵티마이저는 고정된 규칙으로 선택도를 추정하는데, 운이 좋아 그 값이 맞을 수 있지만 십중팔구 틀릴 가능성이 크다. 좀 더 구체적으로 말해, 아래 1~4번은 선택도(Selecivity)를 5%로 계산하고, 5~8번까지는 0.25%로 계산한다.

따라서 테이블에 1,000개 로우가 있을 때 옵티마이저는 1~4번 조건에 대해서는 50개 로우가 출력될 것으로 예상하고, 5~8번 조건절에 대해서는 3개 로우가 출력될 것으로 예상한다.

이처럼 바인드 변수를 사용하면 정확한 컬럼 히스토그램에 근거하지 않고 카디널리티를 구하는 정해진 계산식에 기초해 비용을 계산하므로 최적이 아닌 실행 계획을 수립할 가능성이 커진다.

아래처럼 상수 조건식(no ‘=’ 100, no between 50 and 600)을 사용할 때는 거의 정확한 카디널리티를 계산해낸다.

좋은 실행 계획을 위해서라면 DW, OLAP, 배치 프로그램(Loop 내에서 수행되는 쿼리 제외)에서 수행되는 쿼리는 바인드 변수보다 상수를 사용하는 것이 좋고, 날짜 컬럼처럼 부등호, between 같은 범위 조건으로 자주 검색되는 컬럼일 때 특히 그렇다. OLTP성 쿼리이더라도 값의 종류가 적고 분포가 균일하지 않을 때는 상수 조건을 쓰는 것이 유용할 수 있다.

참고로, 파티션 테이블을 쿼리할 때 파티션 레벨 통계 정보를 이용하지 못하는 것도 바인드 변수의 대표적인 부작용 중 하나다. 파티션 레벨 통계보다 다소 부정확한 테이블 레벨 통계를 이용함으로써 옵티마이저가 가끔 잘못된 실행 계획을 수립한다.

(5) 결합 선택도

아무리 히스토그램을 많이 만들어두어도 두 개 이상 컬럼에 대한 결합 선택도를 구할 때는 정확성이 떨어진다. 특히 3절 옵티마이저의 한계’에서 설명한 바와 같이 조건 컬럼간에 상관관계가 있을 때 그렇다. (5) 결합 선택도 산정의 어려움’ 부분을 상기하기 바란다.

동적 샘플링(Dynamic Sampling)

오라클은 91부터 동적 샘플링을 통해 이 문제를 해결하려고 시도하고 있다. 소량의 데이터 샘플링을 통해 WHERE 조건에 사용된 두 개 이상 컬럼의 결합 분포를 구하는 기능으로서, 동적 샘플링 레벨을 4 이상으로 설정할 때만 작동한다.

다중 컬럼 통계(Multi-column Statistics)

다행스럽게도 11g에서는 확장형 통계(Extended Statistics)라고 불리는 기능을 통해 다중 컬럼에 대한 히스토그램도 생성할 수 있게 되었다.

Database, SQL Tuning

SQLP

This post is licensed under CC BY 4.0 by the author.